Combining student scores

It turns out that aggregating student scores across different subjects is much trickier than most people imagine

In the late 1980s, Paul Black and I co-taught a Masters module on Exploratory Data Analysis, some of which was based on work that Paul had done earlier with Jon Ogborn for Nuffield Physics. One example that Paul shared with me really got me thinking about what happens when we add scores from different subjects (and if anyone can tell me where this example comes from, I would be grateful).

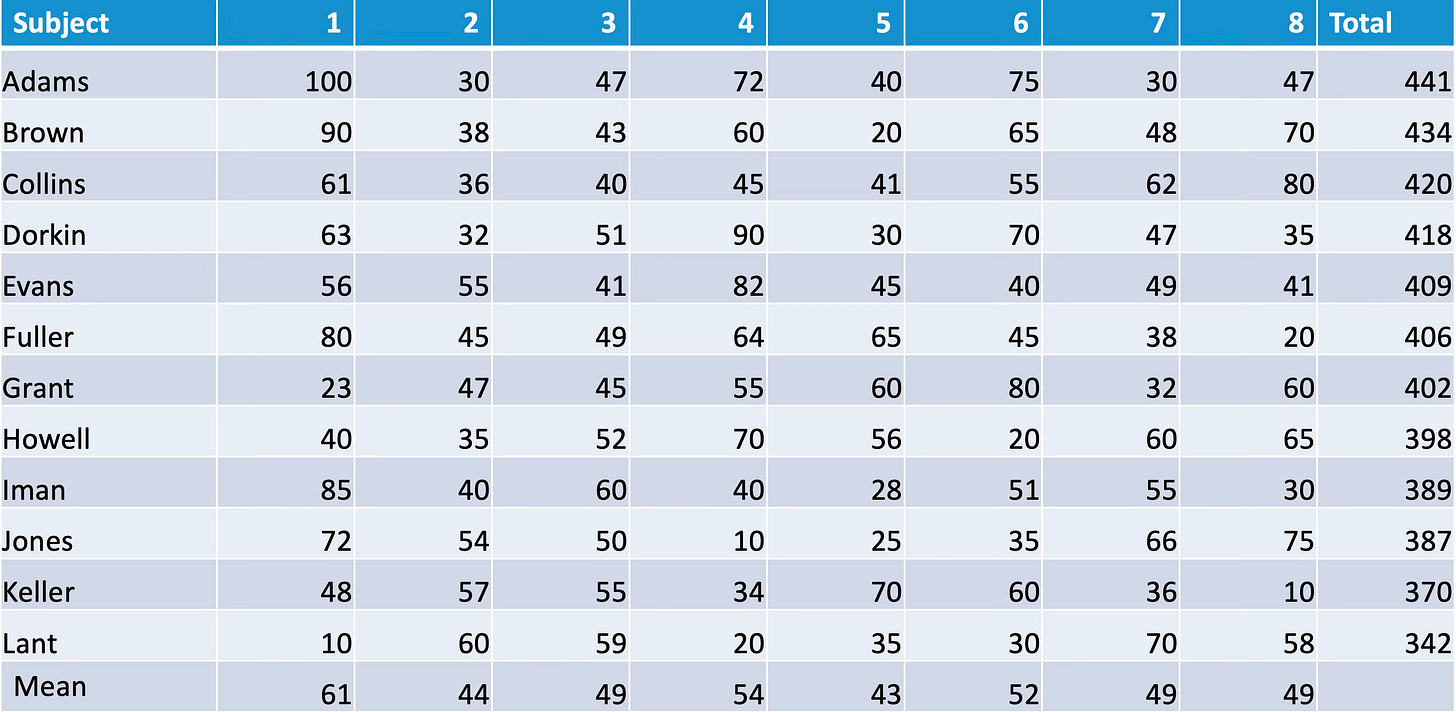
If we have a group of 12 students, and have their percentage scores on 8 subjects, it might seem easy to work out who is the best students. We just add up the scores on each of the 8 subjects, and see who has the highest total:

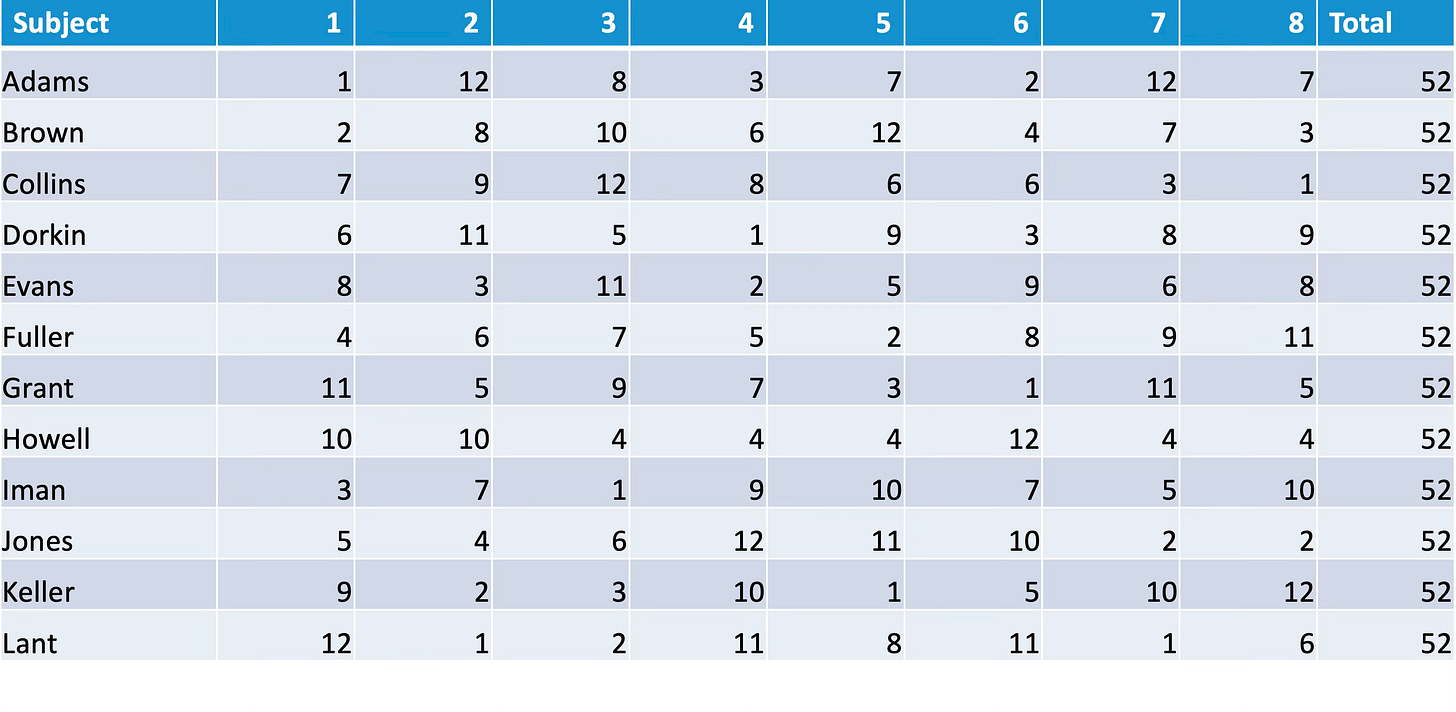
However, there is a problem here. Subject 1 used most of the mark range, with scores ranging from 10 to 100, while others, such as subject 3, have scores ranging only from 40 to 60. To control for this, we could replace scores with class ranks, giving the highest scoring student in each subject a rank of 1, and the lowest scoring student a rank of 12:

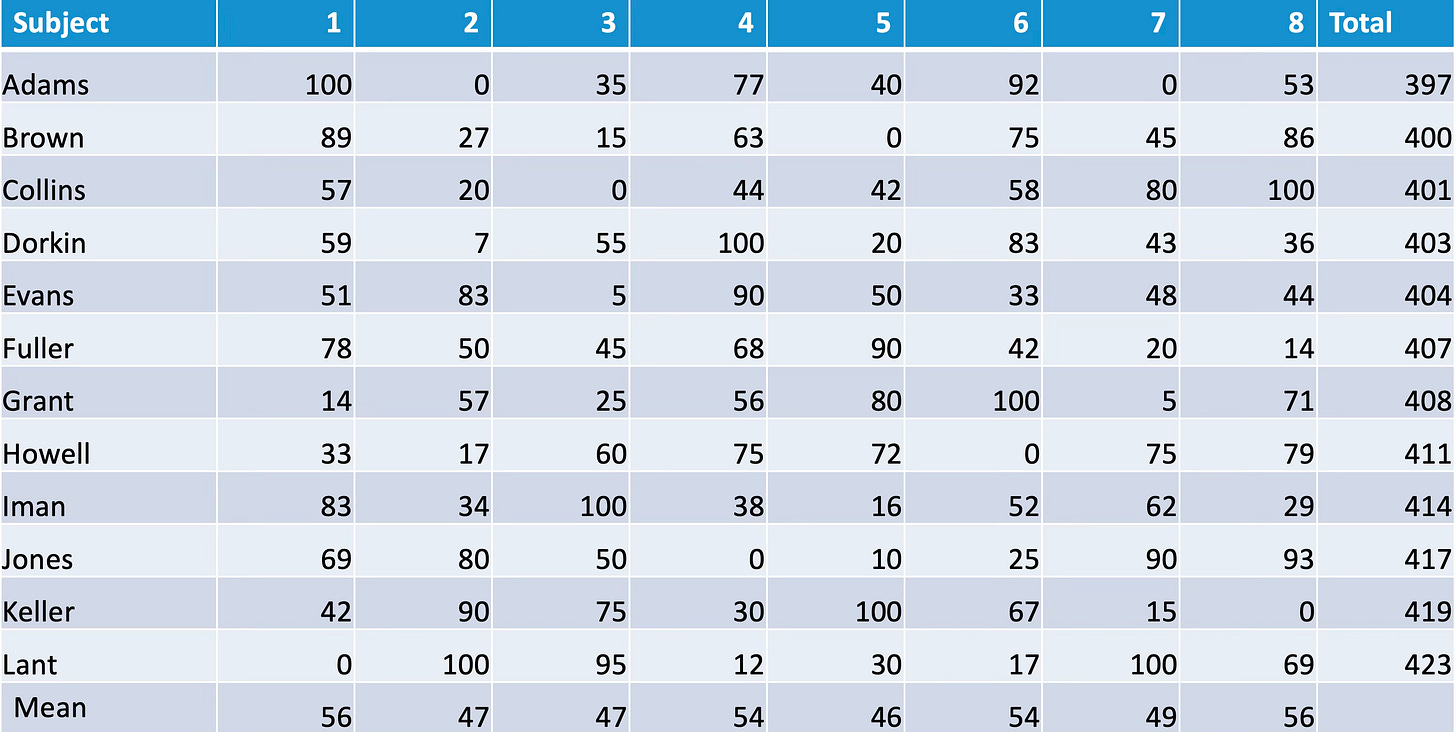
However, when we use ranks, we throw away information, because we take no account of how much better the first ranked student is than the lowest ranked student; the difference will always be 11. Instead, a better approach might be to scale the scores so that every subject uses the full range of scores from 0 to 100, with the lowest scoring student getting 0, the highest scoring student getting 100, and the others scaled in between:

Now, the student who was top—Adams—is at the bottom, and the student who was at the bottom—Lant—is at the top. And if that doesn’t make you realize that adding up scores like this is not as straightforward as it seems, I don’t know what will.